Interdisciplinary Note (1 of 16)
Let's review some basic electricity concepts. A good footing in the fundamentals will make DC current much more transparent. In electrostatics, we describe the behavior of charges interacting through the electric force, the force described by Coulomb's law. We call the electric force "electrostatic" because, unlike magnetic force, it can happen between stationary charges. We can describe the force between two charges, charge X and charge Y, or we might choose to describe the electric field permeating the space surrounding charge X alone. The electric field of charge X gives us a picture of its ability to exert force on any other charge in its vicinity. If X is a positive charge, the we represent the field of X on the page with vectors pointing away from it in every direction. The direction of the field vectors tells us the direction of the force X would exert on any hypothetical positive charge in its vicinity. As the vectors spread out further from X, that tells us the field is getting weaker. If X were a negative charge, the field vectors would be pointing in towards it.
The electric field tells us how many newtons of force would be exerted per coulomb of charge were some charge placed at a particular location. Force applies to a specific interaction between two or more charges while the field describes the ability of one charge or charge distribution to exert force somewhere else, an ability that permeates the space around it.
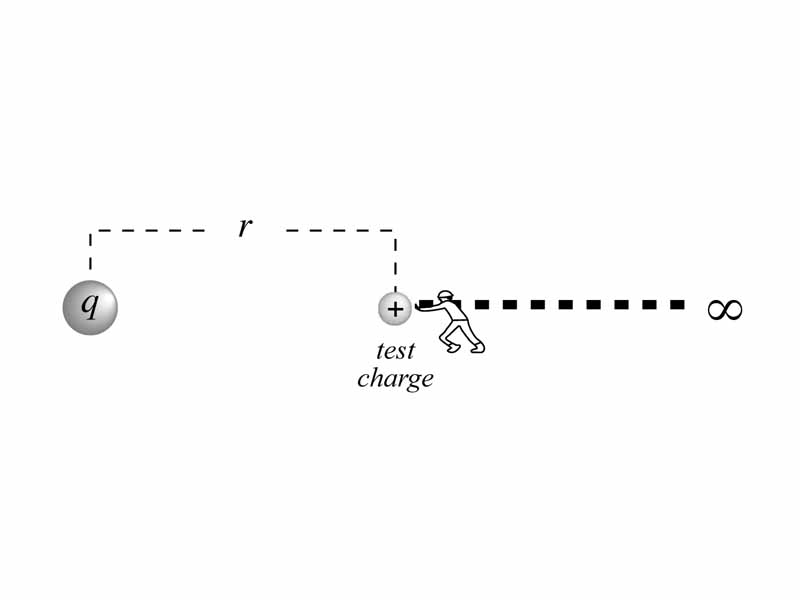
An analogy to this relationship between electric force and electric field extends to the relationship between potential energy and electric potential or voltage. We can describe either the specific electrical potential energy state existing between charge X and charge Y or we can describe the energy properties of the field of charge X alone, the capability the field has to perform work between two points or between a point and ∞. We ask how hard would it be to do work against this field if we were to move a hypothetical charge from one position to another in the field? How many joules of work does it take to move a coulomb of hypothetical charge (joule/coulomb = volt). If we imagine moving a test-charge from infinitely far away to point A near charge X, this is the electric potential of point A. The joules per coulomb required to move from point A to point B gives the potential difference, or voltage, between those two points. The actual potential energy that exists in a situation applies to a specific arrangement of two or more charges while the voltage describes the ability of the field to perform work on hypothetical charges we imagine moving around in the field.
Remember that one volt equals one joule per couloumb - ten volts equals ten joules per coulomb - and think about this when you look at a DC circuit diagram. There is the voltage source. It might be a galvanic cell or some other source of electric potential. On the diagram, it's idealized with a long bar for the positive terminal and a short bar for the negative. If it's a ten volt voltage source, that means that a coulomb of positive charge has ten joules more potential energy when its located at the long bar than at the short bar. Picture electric current flowing through the resistor as a stream of charges falling through through the resister, losing their energy there, making heat or light or doing mechanical work. Picture a conveyor belt lifting rocks up one meter and then letting them drop through a bunch of cymbals making a racket. That would be a DC gravity circuit. A kilogram lifted one meter has 10 joules of potential energy (mgh). Our conveyor belt would be a ten joule per kilogram voltage source. That's how much work the gravitational field performs on a kilogram between the top and the bottom. The power is the voltage times the current (P = VI). If we were moving five kilograms of rocks per second, the power of our gravity circuit would be P = (10 joules per kilogram)(5 kilograms per second) = 50 watts. That would be a 50 watt noisemaker. Hopefully you aren't doing this experiment because the neighbors will be angry.
You can think about electric power the same way. The current represents charges falling through a potential. If you have a 10V voltage source and there is 5 amperes of current, the circuit has a power of 50 watts. (10 joules per coulomb)(5 coulombs per second) = 50 watts.