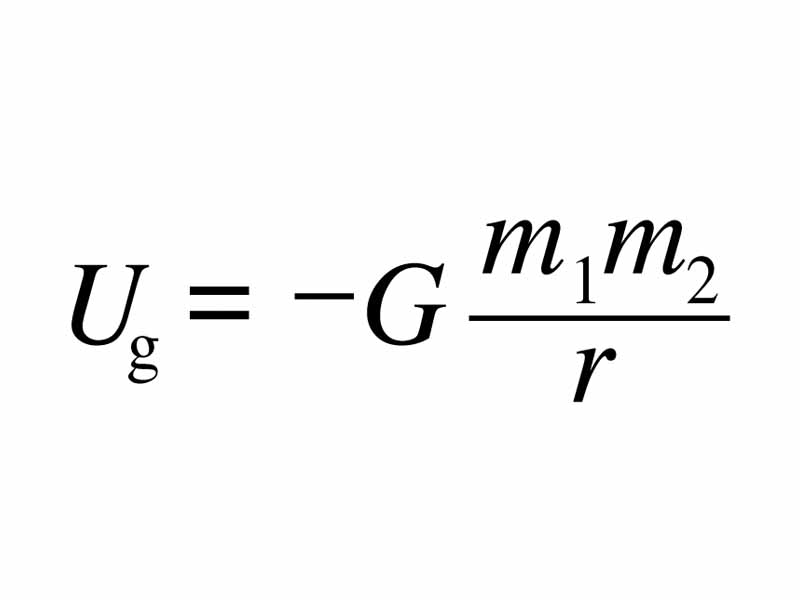When dealing with potential energy changes involving a gravitational system, zero potential energy represents the state of the objects when they are infinitely far apart. All other values are negative. The two masses have fallen together into a well of their mutual binding energy.

As we discussed earlier within Newton's Laws, there are two main types of gravity problems, those in which the gravitational force is virtually constant over the distances involved and those in which the gravitational force changes with varying position within the system.

Each of these different models has a different approach to energy. The manner of describing changes in energy is different in a constant force system versus a system where force changes with position.

In both cases, however, as work is done against or by the field, as the object is changing position, its state of potential energy is changing. As two attracting objects are moved further apart, the potential energy of the system increases whether an object is being raised from the surface of the Earth or whether two objects are separating in outer space.

On the surface of the Earth, where the distances over which the object is going to move will be relatively small, it is more convenient to assign zero as the potential energy on the ground.

For situations in outer space, however, where the force can be seen to decrease the further apart the objects are moved, zero potential energy represents the state of the objects when they are infinitely far apart. All other values are negative. Think about this. Make sure you understand this. If the Earth and Moon were astronomically far apart, the potential energy would be zero. They have fallen together into a potential energy well, which is a negative value. Try to get the equation to tell you this. The book on the table is in a well of gravitational binding energy with the Earth. To get it into outer space would require an input of work at least as great as the distance from this negative potential energy state to zero.

This is very important to understand because the description of the electrostatic potential energy between unlike charges works the same way. The nucleus of an atom and the electron in its orbit have fallen together into a well of electrostatic potential energy. The work required to pull the electron away from the nucleus, to completely separate the two, equals the ionization energy of the atom.