Michaelis-Menten kinetics.

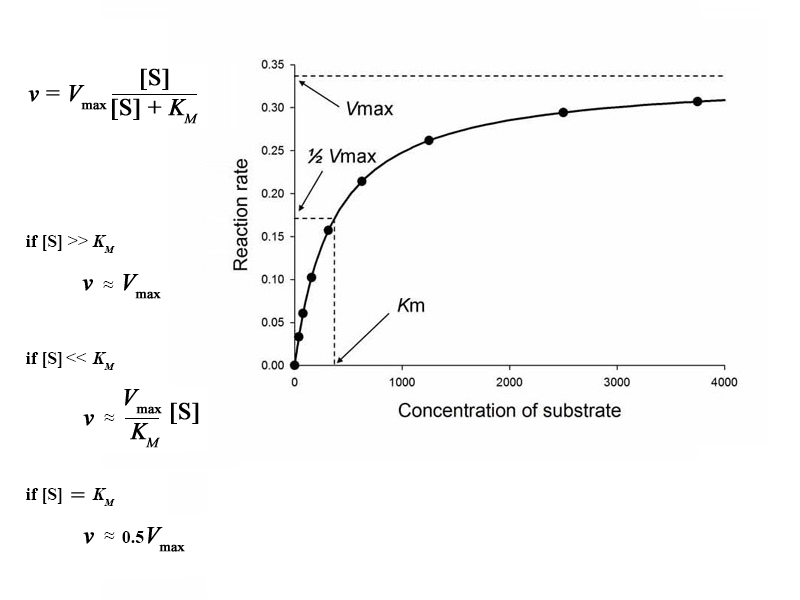
The Michaelis-Menten equation shows the dependence of reaction rate on substrate concentration for elementary enzymatic reactions. In this sense, the Michaelis-Menten equation serves the same purpose for enzymatic reactions as the simpler rate expression from general chemistry does for homogeneous benchtop reactions. However, even for an elementary enzymatic reaction, Michael-Menten kinetics describes a more complex, multistep process in which the enzyme catalyst and substrate bind to form enzyme-substrate complex and then subsequently turn over through the catalytic step of the enzymatic mechanism to form the product (or fall backwards and dissociate, releasing the substrate without forming product). This complexity gives Michaelis-Menten kinetics very different features than ordinary homogeneous kinetics. In an enzymatic reaction, when the concentration of substrate becomes so large as to saturate the enzyme, the rate is maximal (V_max). It becomes independent of substrate concentration. On the contrary, when the concentration is very small, the rate is proportional to substrate concentration.

This portion of the curve where the concentration of substrate is very small compared to the value of Michaelis constant is known as the linear range. Doubling the substrate concentration within this range will double the reaction rate (approximately). Language from traditional kinetics is useful here. In this range the enzymatic reaction is said to obey 1st order kinetics.

Language from traditional kinetics is likewise useful for describing the situation when the enzyme is saturated with high substrate concentration and rate is asymptotically approaching V_max. In this range, the rate doesn't respond to increases in substrate concentration. We say the reaction is obeying zeroth order kinetics.