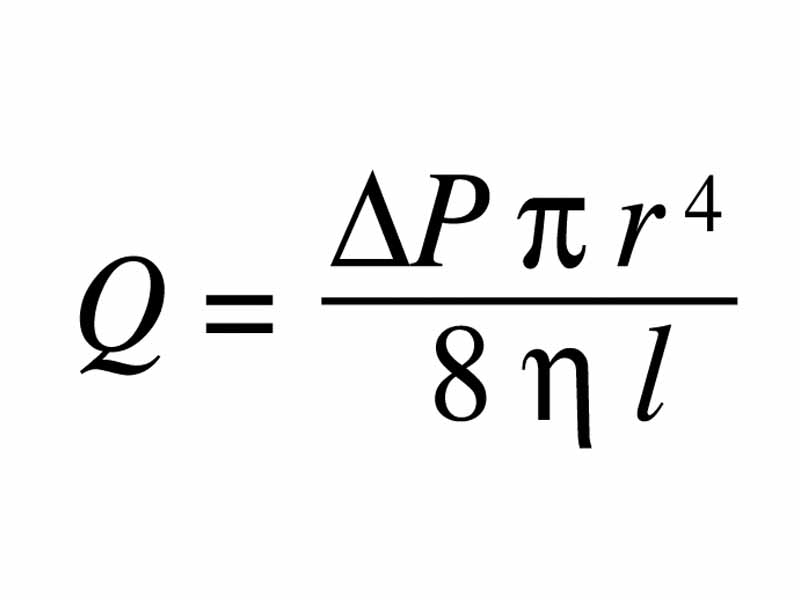Poiseuille's equation describes the pressure drop along a blood vessel due to viscous dissipation.

The fluid dynamics in the human circulatory system are different in many important ways from the flow of an ideal fluid. Viscous resistance applies, and thus Poiseuille's Law applies, and also turbulance is possible in the circulation, which is a deviation from ideal fluid behavior.

Despite deviation from ideal flow, the physics governing the flow of an ideal fluid are definitely helpful for understanding the behavior of fluid in the circulatory system. For example, the continuity of volume flux describes the relationship between the total flow diameter in arteries, arterioles, capillaries and flow speed through those areas. Reasons that the relationship is not exact include the elasticity of blood vessels and the fact that the cardiovascular system is not closed.

Bernoulli's law is also very useful to understand cardiovascular phenomena. For example, Bernoulli''s law helps you understand why pressure is reduced within a stenosis (localized narrowing of a vessel), where flow speed is increased, or pressure is increased within an aneurism (localized dilation or bulge), where flow speed is reduced.